非对称算法 RSA DH 还有ECDH
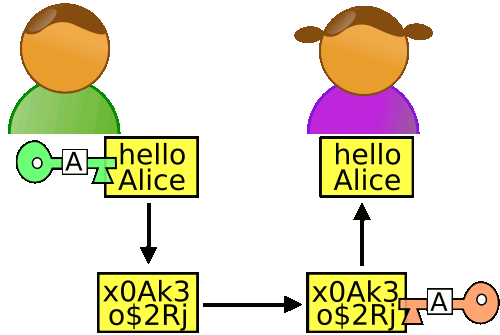
虽然对称算法的效率高,但是密钥的传输需要另外的信道。非对称算法RSA和DH可以解决密钥的传输问题(当然,它们的作用不限于此)。这两个算 法的名字都是来自于算法作者的缩写,希望有朝一日能够出现用中国人命名的加密算法。非对称算法的根本原理就是单向函数,f(a)=b,但是用b很难得到 a。
RSA算法
RSA算法是基于大数难于分解的原理。不但可以用于认证,也可以用于密钥传输。那么用户A和B如何利用RSA算法来传输密钥呢?
1:A产生一个密钥K,用B的公钥加密K,然后将得到的密文发送给B。
2:B用自己的私钥解密收到的密钥,就可以得到密钥。
(感谢网友的提醒,已经修改了)
DH算法
DH算法的出现就是用来进行密钥传输的。DH算法是基于离散对数实现的。用户A和B如何利用RSA算法来传输密钥?
在通信前,用户A和B双方约定2个大整数n和g,其中1,这两个整数可以公开
1) A随机产生一个大整数a,然后计算Ka=ga mod n。(a需要保密)
2) B随机产生一个大整数b,然后计算Kb=gb mod n。(b需要保密)
3) A把Ka发送给B,B把Kb发送给A
4) A计算K=Kba mod n
5) B计算K=Kab mod n
由于Kba mod n= (gb mod n)a mod n= (ga mod n)b mod n,因此可以保证双方得到的K是相同的,K即是共享的密钥。
ECDH算法
ECC 算法用途比RSA还猛,不仅可以加解密、签名验证。还可以与DH结合使用,用于密钥磋商,这个密钥交换算法称为ECDH。交换双方可以在不共享任何秘密的 情况下协商出一个密钥。ECC是建立在基于椭圆曲线的离散对数问题上的密码体制,给定椭圆曲线上的一个点P,一个整数k,求解Q=kP很容易;给定一个点 P、Q,知道Q=kP,求整数k确是一个难题。ECDH即建立在此数学难题之上。密钥磋商过程:
1) Alice生成随机整数a,计算A=a*G。Bob生成随机整数b,计算B=b*G。
2) Alice将A传递给Bob。A的传递可以公开,即攻击者可以获取A。由于椭圆曲线的离散对数问题是难题,所以攻击者不可以通过A、G计算出a。Bob将B传递给Alice。同理,B的传递可以公开。
3 ) Bob收到Alice传递的A,计算Q=b*A
4) Alice收到Bob传递的B,计算Q‘=a*B
Alice、Bob双方即得Q=b*A=b*(a*G)=(b*a)*G=(a*b)*G=a*(b*G)=a*B=Q' (交换律和结合律),即双方得到一致的密钥Q。
算法的复杂度依次提高,ECDH > DH > RSA。 这3中算法都在openssl中有实现,并且自定义其中的素数。
版权所有,禁止转载. 如需转载,请先征得博主的同意,并且表明文章转载自:IT夜班车,否则按侵权处理.